A body immersed in fluid is subject to an upwards force equal to the weight of the fluid displaced.
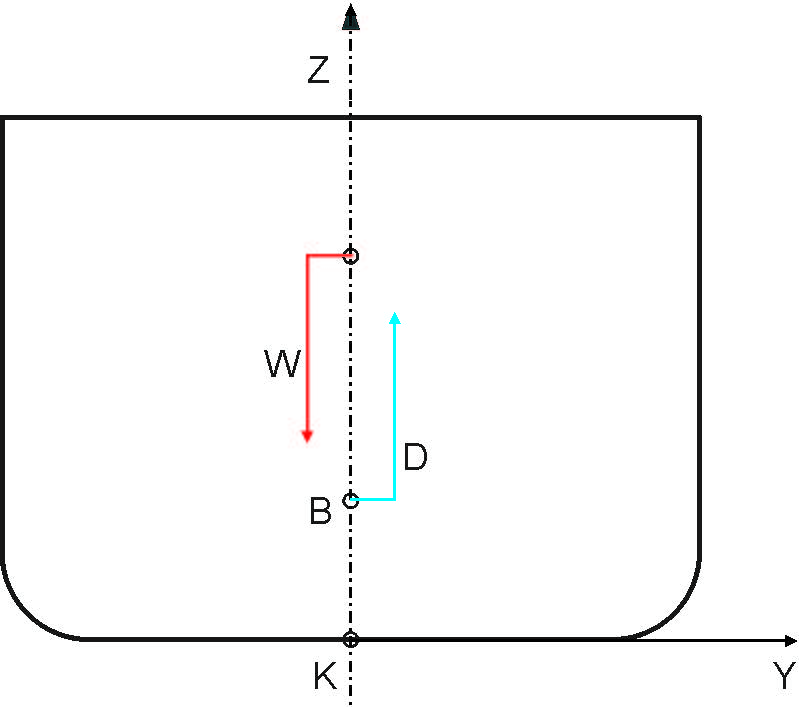
For the ship to float, it must displace its own weight of water: W = D = V x water density, where: W – Weight of the ship, D – Displacement, V – Volume of displacement
The displacement of a ship, D, is defined as the number of tones of water it displaces. The volume of displacement, V, is the underwater volume of a ship afloat i.e. the volume below the waterline.
G – Centre of gravity, B – Centre of buoyancy
Two vertical forces always act upon the ship when rest in still water: its weight, W, acting downwards through the centre of gravity, G, and the displacement, D, acting upwards through the centre of buoyancy B. The weight and the displacement are equal in magnitude. For the ship in equilibrium the sum of their moments must be zero. Therefore the ship will heel and trim as long as centres of gravity and buoyancy will be in the same vertical line.
